力と運動方程式 z 力の単位 N(ニュートン) この方程式 (微分方程式) はどのように解く? ⇒ 球の位置 x が t とともにどのように変化? よく出る方程式 実験で微分方程式を解く t dt d t t dt d t t dt d t t dt d t α α α α α α sin cos cos , sin sin cos cos , sin =− = =− = 周期的に振動する解 ⇒ sin と書けます。以下では、力 は時間と座標に依らない定数とします。 連立1階微分方程式へ変形 ¶ ニュートン方程式は2階の微分方程式ですが、SciPyなど多くのライブラリは連立1階微分方程式 を解くように設計されています( 常微分方程式の解法 を参照) 。 そこで、ニュートン方程式を連(x n,f(x n))を通り、傾きがf'(x n)の直線方程式は!

道具としての微分方程式 野崎 亮太 著 紀伊國屋書店ウェブストア オンライン書店 本 雑誌の通販 電子書籍ストア
ニュートン 微分方程式
ニュートン 微分方程式-微分方程式 第4回 (全15回) 横田 孝義 19年5月9日(木) 2 14 モデル化:分離可能な方程式 例1 放射性炭素による年代測定 骨を採掘 放射性炭素の含有量が現在の生物の骨の含有量の 25%だった。放射性炭素の半減期は5730年である。 𝑦′= 𝑦, 𝑦 =𝑦0 𝑘𝑡 半減期は5730年である。 𝑦0 5730𝑘= 1回答 物理に量子とかニュートンとか古典とかあるわけではありません。 ものの見方として、取り扱い方として量子力学やニュートン力学という手法があるだけです。対象と目的に応じて正しい取り扱い方を選択するわけです。 もし、ニュートンの方程式をつかうならば、それは量子力学的




大学数学 微分方程式入門 微分方程式とは Youtube
(2)式を用いると、ニュートンの運動方程式(1)は、 m d⃗v dt = F⃗ (3a) あるいは m d2⃗r dt2 = F⃗ (3b) とも表せる。(3a)式や(3b)式は、数学的には微分方程式と呼ばれる。物体の速度⃗v や位置⃗r を求め ることは、数学的には微分方程式を解く(=積分する)作業でSinϕ 一般化されたGS方定式 以上から,次のようなPoisson型方定式が得ら れる. ∆(Aϕ sinϕ) = S sinϕ, S = − κ′H ϕ 4πρRµ4πρR3ΩΩニュートン力学は微分方程式論, 相対性理論は微分幾何学とそれぞれ関係する また, 量 子言語は作用素代数と関係する(cf 文献KOARA 18;
コペン) ことは当然だろう さて, (B1) デカルト哲学はデカルト座標と関係するのか? は愚問である2.微分方程式系に対するニュートン図形は? 疑問次の正規型で与えられた方程式系のニュートン図形は? L = zp1 d dz IN −A(z) (p ≥ 1), A(z) = (aij(z))i,j=1,2,···,N 考察1)特性多項式 det {zp1ζI N −A(z)} = znp(zζ)N ∑N j=1 aj(z)(zζ)N−j を用いて、単独作用素と同じようにして考える方法。変数係ニュートンの運動方程式とラグランジュの方程式 概要 ニュートンの運動方程式は、座標変換すると式が変わる。そして、その計算は大変である。その計算を軽 減するために、ニュートンの運動方程式と同値な方程式を利用する方法がある。ただ、それができることを 示すこと自体は大変な事�
d 3,0 は、3回微分したものになります。 すなわち、d r,k は、点 (x k,y k )を起点とするr階の階差分商であり、ニュートンの補間法の公式は、階差分商を係数にした多項式だといえます。11 位置速度加速度 12 第2法則(ニュートンの運動方程式) 13 第1,第3法則 14 例題(位置r(t)から力F(t)を求める)授業のページ§25 ニュートンの運動方程式と不定積分 81 §25 ニュートンの運動方程式と不定積分 ニュートンの運動方程式は『プリンキピア』(1687) の中で述べられた運動 の第2 法則(☞p61)にその起源がある:運動の量(=質量m ×速度 v)の 変化(=質量m ×加速度 a)( a(t) = d v(t) dt) は,加えられた力
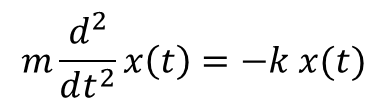



Step 05 2階常微分方程式を解いてみる ニュートン方程式 筑波大学原子核理論研究室




My Notebook 数学 微分方程式 Note Md At Master Yagami360 My Notebook Github
微分方程式ニュートンの冷却の法則を表す微分方程式は で表されます。 ここで 変数 は時間、 読者になる 倭算数理研究所 科学・数学・学習関連の記事を、「倭マン日記」とは別に書いていくのだ! トップ > 熱力学 > ニュートンの冷却の法則ニュートン方程式 十河 清 1 力学を学ぶ―私の経験から この「ニュートン方程式」の原稿依頼が私のと ころに舞い込んだのは,最近「ゼロからの大学物 理」シリーズの一つとして『力学i, ii』1) を書いた ばかりなので,執筆経験の感想とか,やむを得ず ボツにした事柄など,腹に溜ったもの ニュートン法とは? 図解"近似値"が求まる仕組み 其の1:適当な値をとって (x,f (x))を求める 其の2:接線を引く 其の3:接線とy=0との交点を求め→新たに接線を引く 其の4操作を繰り返す ニュートン法の証明問題を解いて理解 ルート5の近似値を




微分と積分 改訂第2版 ニュートンプレス



書籍紹介 微分方程式と数理モデル 遠藤雅守 北林照幸 共著 数学
微分係数と傾きの定義の関係を利用して導出します。 @see 優技録 分数の式変形 漸化式が出来た。 これをループさせていくと目的の解に限りなく近く微分方程式と物理 森 真 10月23日から11月13日 を考えました.微分の先陣争いはニュートンのイギリスとライプニッツのド イツと国家を巻き込んだ争いになったことは有名です.どの時代にも名誉欲 に目がくらんだ人間というものは存在するものです. さらに,ニュートンが万有引力の法則微分方程式 第6回 (全15回) 横田 孝義 17年5月19日(金) 2 授業計画 4/14 4/21 4/28 5/8 5/12 5/19 5/26 6/2 6/16 6/23 6/30 7/14 7/21 7/28 7/7 中間テスト 3 14 モデル化:分離可能な方程式 例1 放射性炭素による年代測定 骨を採掘 放射性炭素の含有量が現在の生物の骨の含有量の 25%だった。放射性炭素の半減期は



Nekodamashi Math Blog Ss Blog Jp



ニュートン冷却の法則を使った時刻予想の問題 ある事件の被 Yahoo 知恵袋
ニュートン力学は、質点の運動に対する以下の3つの法則にまとめら れる。 第一法則慣性の法則 動が記述される。 ニュートン力学の際立った特徴は、運動法則が2階の微分方程式 m d2r dt2 = F (11) で与えられていることである1。つまり、ある時刻での質点の位置と速度 r, dr dt (12) が与えられるその際に、微分積分法の整備にとどまらず、新しい概念で ある「変分」(variation) という考え方が導入された(変分については、第3章で詳しく議論する)。「初め に運動方程式ありき」ではなくて、変分原理によって運動方程式が「導出される」のである微分を使って力学に挑戦しよう ―万有引力の証明 コラム 和算の中の微積分 5 発展編 水谷仁の微積分講義(1) コラム ネイピア数とは何か 水谷仁の微積分講義(2) 世界を理解するための鍵となる「微分方程式」 コラム 微積分は何の役に立つ? 新たな楽器や




大学数学 微分方程式入門 微分方程式とは Youtube



42 5 ニュートンは何故微分方程式を使わないで プリンキピアを書いたのか 理系の科学哲学 コペンハーゲン解釈 理系の西洋哲学史
P > の 時間による微分は となります. つまり,量子力学では, 「粒子の 運動量の平均値の 時間変化は, 粒子に働く力の平均値 に等しい」 という エーレンフェスト の定理 が成り立ちます. この定理 (8) 式と ニュートンの運動方程式 (3) とは,同形であることに 注意してください. この意味 第67回 微分・積分の数学 ニュートン・ラフソン法 前編 09年9月24日 平田敦 数学, Java, 微分, 積分, ニュートン・ラフソン法, 関数 この記事を読むのに必要な時間:およそ 2 分 1 2 離れたところに飛んでくるテニスボールに対して, プレイヤーは先ず 微分方程式 (1)の解 は力 の作用を受けている質量 の物体の運動を表しています。 したがって、物体に働く力 の作用を受けている質量 の物体の微分方程式であるニュートンの運動方程式を解くことができます。 2 自由落下を事例に解を求める 2階の微分




微分方程式




ヤガミ 微分方程式 より ニュートンラプソン法 数値解析 微分方程式 Differentialequation 常 微分方程式 Ordinarydifferentialequation 数値解析 Numericalanalysis Newtonraphsonmethod T Co Gfhmz1mnrp
数値微分 の手法としてよく知られている 二分法 と ニュートン法 の違いを説明します. 二分法は,解を含む区間の中間点を求める操作を繰り返すことで方程式を解く反復法による求根アルゴリズムです. 二分法は1次収束なので収束(Convergent)までが ニュートン法の導出 f (x)の微分すると導関数の f ' (x)が出る;ニュートン重力でのGS方程式 の 左辺のΨをAϕ(= Ψ/R)に,微分 演算子をラプ ラシアンに書き換える. ∆(Aϕ sinϕ) = ∂2A ϕ ∂R2 1 R ∂Aϕ ∂R − Aϕ R2 ∂2A ϕ ∂z2!




最強に面白い 微分積分の通販 髙橋秀裕 紙の本 Honto本の通販ストア




Masahiro Hotta 一般の量子状態を初期状態にすると 時間に関して2階微分方程式であるニュートン方程式 は出てきません その本の主張とは異なり ニュートン方程式が出てくる条件は 場の量子論の繰り込みと全く関係がありません
ニュートンの運動の第2法則 Isaac NEWTON (1642 1727) ma = f 微分方程式で書くと m dv dt = f または m d2r dt2 = f 0 x y v 0 2次元放物運動!2微分積分学を確立したニュートン(Sir Isaac Newton, 1642–1727) が微分方程式の創始者と考えられる。 3 まず空気抵抗が無視できるとする。 また重力加速度は本当は場所により変化するがそれも無視す回答 (2件中の1件目) 運動方程式が2階微分方程式で書かれ, 通常の運動解析はそれで足りるから, 3階微分を見ることがほとんどありません。ところが, 加速度の時間微分は躍度 (jerk) と呼ばれています。形式的に, 躍度は, {\mathbf j} = \dfrac{{\rm d}{\mathbf a}}{{\rm d}t} = \dfrac{{\rm d}^2{\mathbf v}}{{\rm d}t^2} = \dfrac




星の本棚




ヤフオク 力学と微分方程式 本 雑誌 の中古品 新品 古本一覧
X˙ =u 0 y˙ =v 0 −gt! ニュートン法とは、f (x)=0になるようなxを求めるアルゴリズムの1つで、方程式の解を近似的に求めることができる方法です。 ニュートン法を用いると、√2の値やsin (x)=05になるようなxの値など近似的に求めることができますAmazonでのNewton別冊『微分と積分 新装版』 (ニュートン別冊)。アマゾンならポイント還元本が多数。作品ほか、お急ぎ便対象商品は当日お届けも可能。またNewton別冊『微分と積分 新装版』 (ニュートン別冊)もアマゾン配送商品なら通常配送無料。




文系のためのめっちゃやさしい 微分積分 ニュートンプレス



ニュートンの運動方程式 F maの微分方程式を解いた式を探して Yahoo 知恵袋
数学的には正準方程式というものはラグランジュ方程式という微分方程式を他の座標で表したものにほかならない。この章でも例を多く入れたが適宜飛ばしてもらえば良いと思う。この章の内容自体は難しくないと思う。 41節 ルジャンドル変換 数学でのルジャンドル変換の正しい定義につい いわゆる Newton 運動方程式 時間方向に二階微分が入る時間発展問題の常微分方程式といえば、高校時代に学ぶ Newton の運動方程式がまずは挙げられよう. そこで、ここではそれを扱ってみよう. 具体的には、バネでぶら下げられている重りの挙動を例とし ニュートン法の実装 # (解を求める方程式, 初期値, 微分で用いる微小量, 許容(絶対)誤差, 反復の最大数) def newton_method (f, x0, h= 1e4, tol= 148e8, maxiter= 50) for cnt in range (1, maxiter 1) # 中心差分で微分を求める df = (f(x0 h) f(x0 h)) / (2 * h) next_x = x0 f(x0) / df # 反復回数, 解の近似値x, f(x)を表示 print ('{2d




Newton Method For Stochastic Differential Equations From A Heuristic Algorithm Formulation To The Second Order Convergence By Kazuo Amano




ラグランジュ力学入門
導関数 f ' (x)にX1を入れると f ' (X1)、X1の時の 「傾き(微分係数)」が出る。;ニュートン力学において,運動の第二法則を式で表わしたもので,質点の運動の様子を決める微分方程式である。 質量 m の物体に力 f が作用したときの物体の加速度を a とするとき,直角成分を a=(a x ,a y ,a z) ,f=(f x ,f y ,f z) と書けば,運動方程式および成分式は ma=f ,ma x =f x ,ma yのとき(x軸との交点)なので y=f'(x n)(x−x n)f(x n) x n1 =x n − f(x n) f'(x n




ニュートン力学と微分方程式の意味がわかる Beret Science 大上 雅史 本 通販 Amazon




微分方程式 星の本棚
「微分方程式の解きかた」にかなりのスペースを割く。これはこれでいいのだが、いっぽうで力学 そのものの論理がぼやけてしまうという難点もある。 力学そのものの論理とは、物体の運動がニュートンの運動の三法則という普遍的な法則と個々の 状況に応じた力の法則だけから導かれると偏微分が関係しない微分方程式を、『常微分方程式』と言います。 一変数関数の偏微分は常微分なので、常微分方程式は偏微分方程式の一 種とも言えます。ニュートン方程式が常微分方程式なので、力学では常 微分方程式を解くことがほとんどです。有名なニュートンの運動の法則です。第2法則が所謂運動方程式 に対応します。 微分やベクトルを使う訳(レベル1) (\ref{EOM})式はベクトルの微分方程式です。 なぜ、ベクトルや微分を使う必要があるのでしょうか。 結論から言うと、物体の運動を記述するために、 ベクトルや微分が都合がよい



Comp Tmu Ac Jp




意外と身近な数理モデル 微分方程式 新刊ピックアップ 技術評論社
X=u 0t y =v 0t− g 2 t2 一様な重力場 (重力加速度 ) の中で, 原 点から初速度 で打ち上げた ボールの運動を求めよ g v 0 =(u 0,v 0) m d2r dt2 mg =f f =(0,−mg)!ニュートンの運動方程式 (ニュートンのうんどうほうていしき、 英 Newton's equation of motion )は、 古典力学 において、 物体 の非 相対論 的な 運動 を記述する以下のような 微分方程式 である : m a = m d 2 r d t 2 = F {\displaystyle m {\boldsymbol {a}}=m {\frac {\mathrm {d• ある点x nでの導関数f'(x n)が与えられるとき、!



Course 応用物理学 Industrial And Applied Physics 学部専門 の授業紹介コース




ニュートン力学 Wikipedia
ニュートン法はある方程式f(x) = 0の実数解を求めるための方法です。例えば$ f(x) = x ^ 3 2 $ にすると$ \sqrt3{2} $の値を知ることができます。微分を少し使います。 概要 全体的な流れは次のような感じです 1 初期値$ x_0 $の設定 2 $ n = 0 $とする 3 $ f(x) $の$ x_n $でのを接線求める。方程式は$ y f(x223 変数分離型微分方程式 224 線形二階微分方程式 225 極座標の微分方程式 2a1 アイザック・ニュートン 2a2微分と積分の統一 Column 4 積分するとあらわれる 積分定数「C」とは? 記号の意味 微分積分学の基本定理を実感 微分・積分の歴史 微分方程式 2 もっと知りたい!微積分の発展史 Prologue 科学にいくつもの"革命"をおこしたアイザック・ニュートンの生涯




11 号 電力システムの安定平衡点算出装置 Astamuse



偏微分方程式を使った音響モデリングを学ぶ Wolfram言語 12の新機能



ニュートン りんご
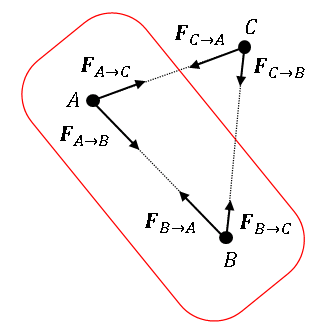



ニュートンの運動方程式と運動量保存の法則



ラプラス変換 微分方程式 フーリエ変換との関係 空間情報クラブ 株式会社インフォマティクス




物理学b Er



加速度運動している車両の微分方程式 制御工学の基礎あれこれ




物理数学演習 第 06 回 1階微分方程式 他の形 の演習 1 次の微分




行列で表記された微分方程式 状態方程式 の解き方 理系大学院生の知識の森




オイラー ラグランジュ方程式 Wikiwand



微分方程式




楽天ブックス 道具としての微分方程式 野崎亮太 本
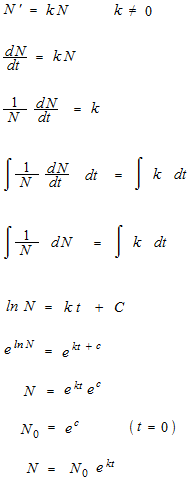



191 ニュートンの冷却の法則 Tokyomaths Com
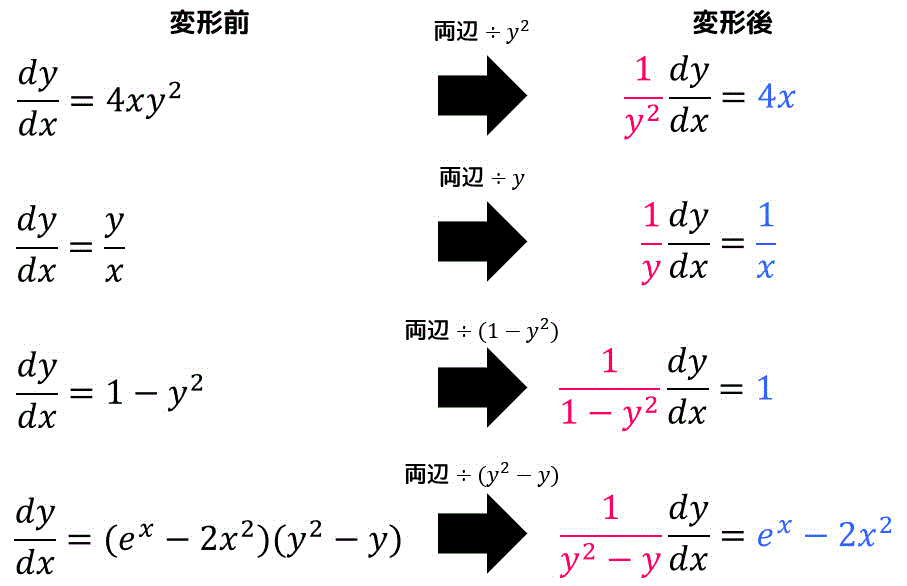



うさぎでもわかる微分方程式 Part01 変数分離形 1階微分方程式 工業大学生ももやまのうさぎ塾



応用力学同演習 Eu



微分方程式の問題なんですがわからないので教えてください ニュートンの冷却 Yahoo 知恵袋
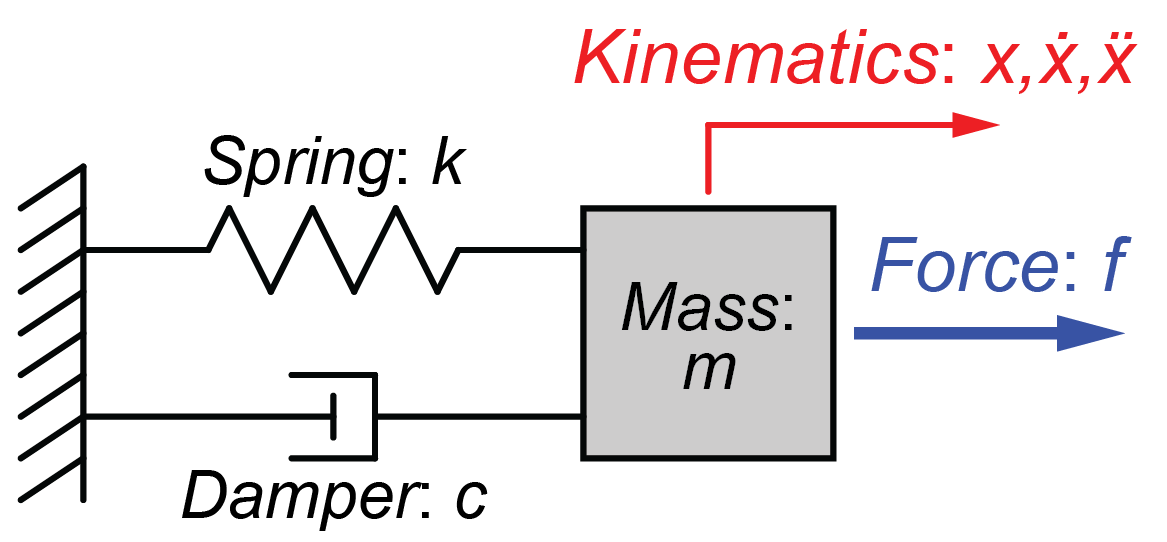



質量 ばね ダンパーシステムを線形微分方程式で表す Tajima Robotics



7 微分方程式 力学系 多様体



ねむねこ幻想郷




My Notebook 数学 微分方程式 Note Md At Master Yagami360 My Notebook Github
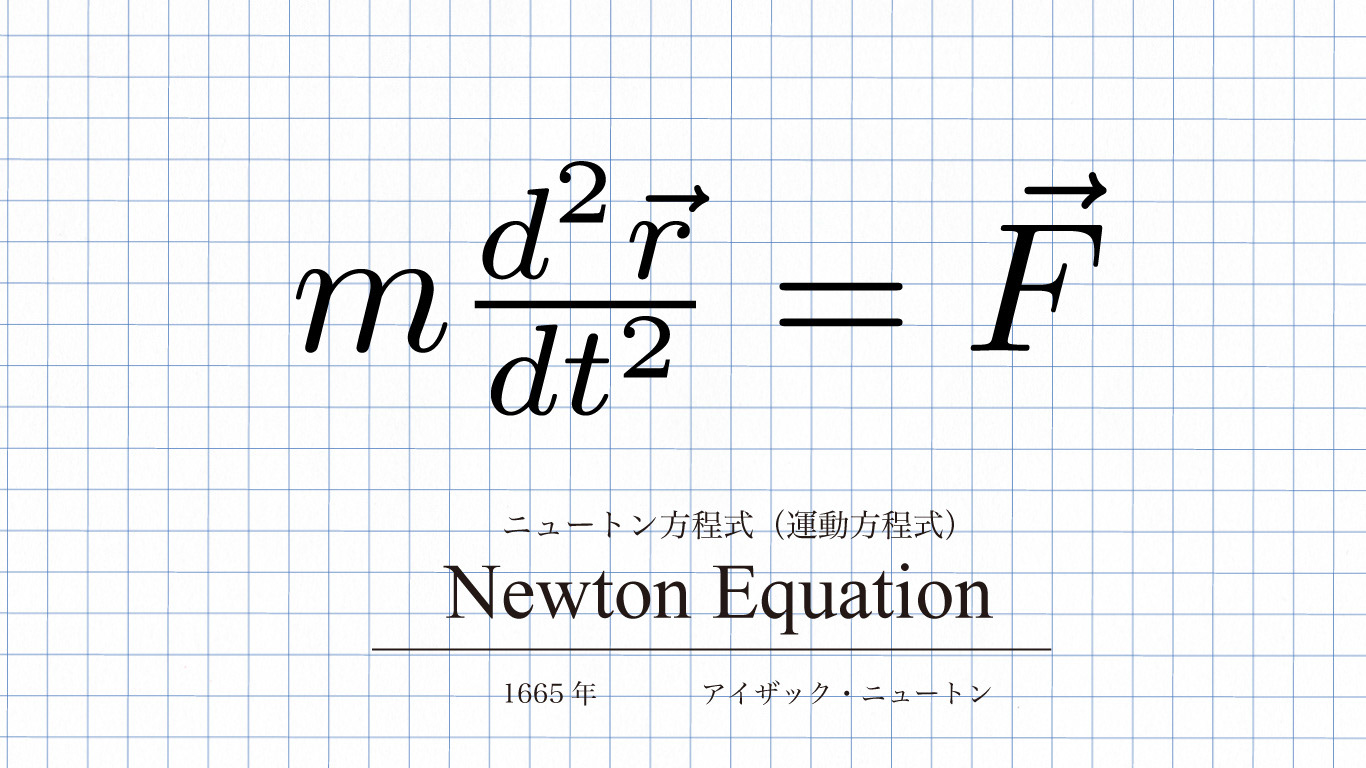



数式の美術館 Physics As Art 加藤雅貴 Masakikato カタカナ数式 Katakana Equation Newton Equation Ver




ニュートン力学と微分方程式の意味がわかる Beret Science 大上雅史 物理学 Kindleストア Amazon




解析学図鑑 微分 積分から微分方程式 数値解析まで Ohmsha




制約条件のない最適化 非線形方程式の解法 Wolfram言語ドキュメント




Newton別冊 微分と積分 新装版 ニュートン別冊 本 通販 Amazon
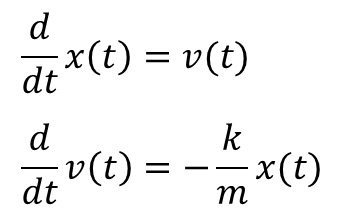



Step 05 2階常微分方程式を解いてみる ニュートン方程式 筑波大学原子核理論研究室



微分積分




Euler法で常微分方程式の数値解放をしましょう This Is Me Trying To Translate My By Siddik Acil Medium




パラメトリック微分方程式 Mathematica 9の新機能




力学 微分とnewtonの運動方程式 高校数学




道具としての微分方程式 野崎 亮太 著 紀伊國屋書店ウェブストア オンライン書店 本 雑誌の通販 電子書籍ストア




5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 ページ 2 3 Study Z ドラゴン桜と学ぶwebマガジン




微分方程式としてのニュートンの運動方程式 Vis Tech




3つの運動方程式 小人さんの妄想
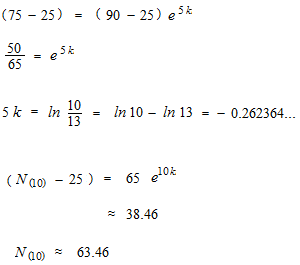



191 ニュートンの冷却の法則 Tokyomaths Com




5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 ページ 2 3 Study Z ドラゴン桜と学ぶwebマガジン




ニュートンの大発見 微分と積分は逆関係 Youtube



Newtonの運動方程式運動方程式を再発見しろと言われたら どうやって発見しますか Quora



Kspub Co Jp




道具としての微分方程式 偏微分編 式をつくり 解いて 使える ようになる 漫画 無料試し読みなら 電子書籍ストア ブックライブ
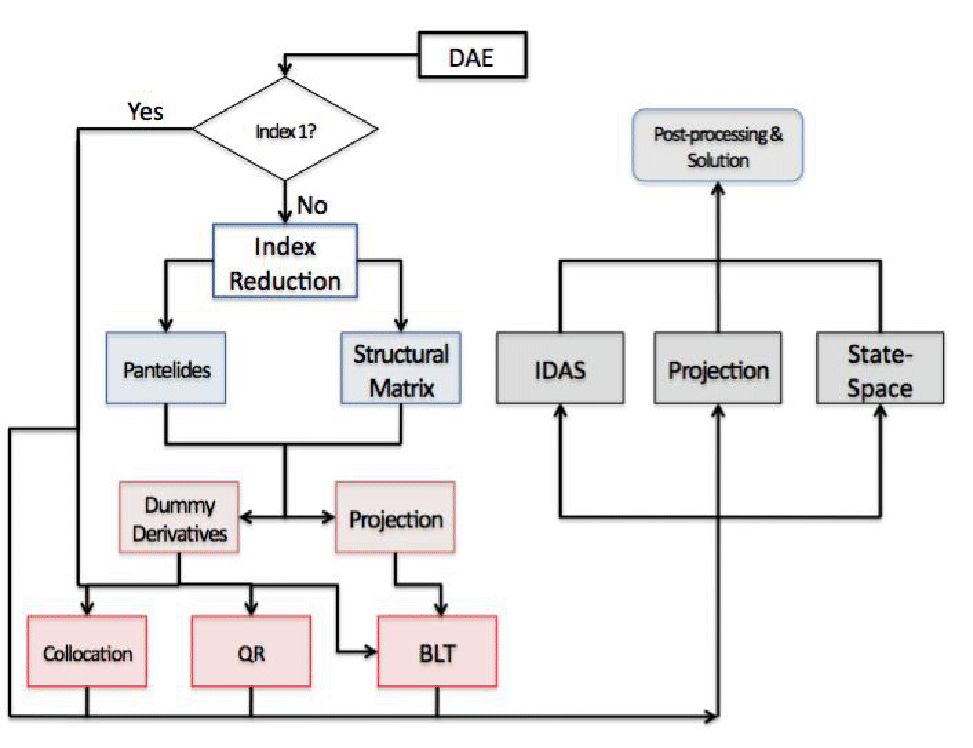



微分代数方程式の数値解法 Wolfram言語ドキュメント




ニュートン力学と微分方程式の意味がわかる 書籍案内 ベレ出版



Kitasato U Ac Jp



計算科学をはじめよう ニュートンの冷却法則 世界はフラクタル




ヨドバシ Com ニュートン力学と微分方程式の意味がわかる 万有引力から相対論的力学まで 単行本 通販 全品無料配達




応用数学 微分方程式の応用例 力学編 微分方程式 りけいのり




力学 1 スケールの話 2 いろいろな力 3 3次元空間内の運動の表現 動径ベクトル 4 速度ベクトル 加速度ベクトル Ppt Download




11 号 電力システムの安定平衡点算出装置 Astamuse



2 微分方程式としての運動方程式



楕円軌道とケプラー方程式 Kepler Equation




5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 Study Z ドラゴン桜と学ぶwebマガジン




微分方程式と物理 Systemtradingのブログ




Euler法で常微分方程式の数値解放をしましょう This Is Me Trying To Translate My By Siddik Acil Medium



ラプラス変換 微分方程式 フーリエ変換との関係 空間情報クラブ 株式会社インフォマティクス
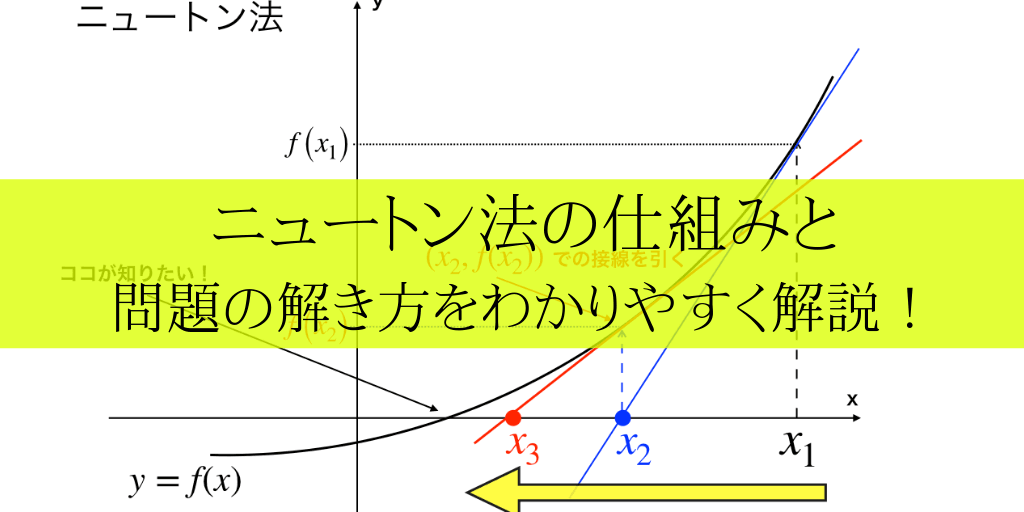



ニュートン法の仕組みと証明の仕方を分かりやすく解説



素人考えの数学論 微分方程式2 鹿児島alien 旧東京から鹿児島へ




テスタを用いた微分方程式の実験 Manualzz




ニュートンとパンデミックの関係 ペスト流行下 育まれた創造 年11月号 事業構想オンライン



微分積分 運動を語る数学の共通言語 空間情報クラブ 株式会社インフォマティクス
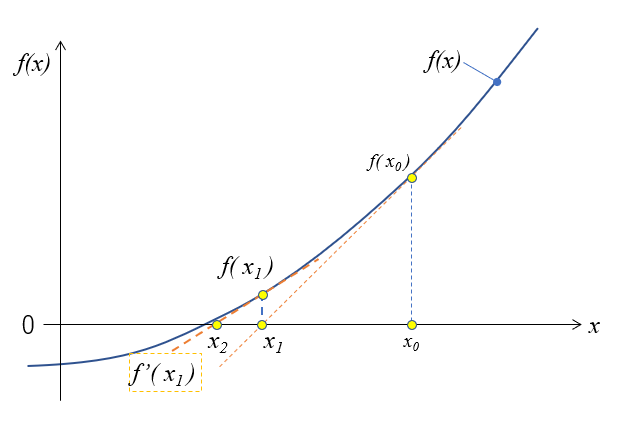



平方根を数値計算で求める ニュートン法 仕事と投資とあと何か




力学演習 Sp
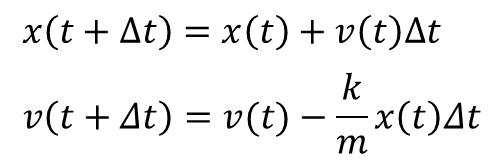



Step 05 2階常微分方程式を解いてみる ニュートン方程式 筑波大学原子核理論研究室



微分積分 運動を語る数学の共通言語 空間情報クラブ 株式会社インフォマティクス




ニュートン力学と微分方程式の意味がわかる 大上雅史の本 情報誌 Tsutaya ツタヤ




Masahiro Hotta 一般の量子状態を初期状態にすると 時間に関して2階微分方程式であるニュートン方程式 は出てきません その本の主張とは異なり ニュートン方程式が出てくる条件は 場の量子論の繰り込みと全く関係がありません
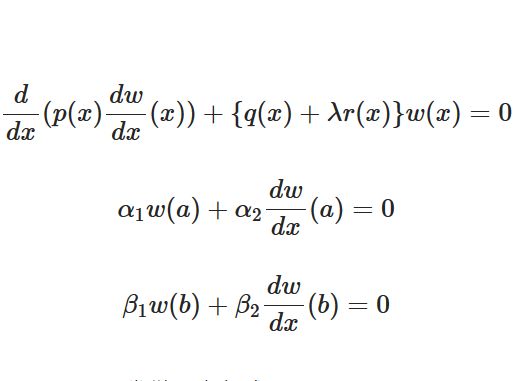



ストゥルム リウビル型微分方程式の発見 熱方程式から 趣味の大学数学



42 5 ニュートンは何故微分方程式を使わないで プリンキピアを書いたのか 理系の科学哲学 コペンハーゲン解釈 理系の西洋哲学史



回転運動の運動方程式




ニュートンとライプニッツの微分積分 離散と連続から考える 書籍案内 技術評論社




ヤガミ 微分方程式 より ニュートンラプソン法 数値解析 微分方程式 Differentialequation 常 微分方程式 Ordinarydifferentialequation 数値解析 Numericalanalysis Newtonraphsonmethod T Co Gfhmz1mnrp



第8回 運動の法則 そもそも ボールが飛ぶってどういうこと 授業報告 科学教育プログラム Event Driven Science




微分方程式の解説と物理 化学への応用記事総まとめ




ヤフオク 方程式 本 雑誌 の中古品 新品 古本一覧




ニュートンの冷却の法則
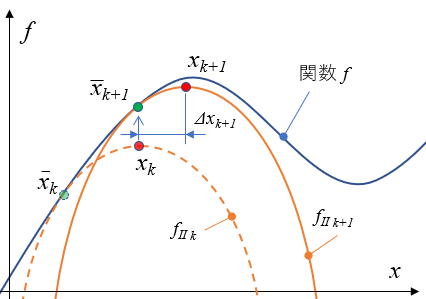



ニュートン法はどのように収束していくのか 1変数の場合で視覚化 仕事と投資とあと何か




ニュートン法 数値計算 Youtube




終端速度型の微分方程式を習得して高校物理を見える化しよう




プログラミング 解けない方程式を解きたい 数値解析 ニュートン法 りけいのり



ニュートン 求め方



三石 数学塾 コーヒーは何度か



0 件のコメント:
コメントを投稿